Overview
The Game AI Framework is a project focused on artificial intelligence in video games. It is built on a framework using Raylib for windowing and 2D rendering, along with an ECS system in C++. The project extends AI components to implement various techniques and concepts such as dynamic vectorial movement with steering behaviors, pathfinding, decision-making using behavior trees, etc.
This project is aimed at enhancing knowledge and skills in video game AI development while developing and extending the framework and is inspired by various sources, including the book "AI for Games" by Ian Millington, videos by Professor Retroman, and "Game AI Pro," among others.
Movement
In the 1980s, movement in video games was achieved using velocities along orthonormal axes, incrementing or decrementing pixel positions to navigate the screen. Today, this has changed, and we use vector spaces for movement. This means objects move via a direction vector and an orientation angle. Thanks to this change, we can not only move along the axes but also diagonally.
Kinematic Movement
Kinematic movement relies on updating positions using velocities within vector spaces. These vector spaces are continuous, which means we should use types like float or double to represent their values, even though they don't provide true continuity but are the closest approximations we have.
Given this, if our framework operates with unsigned types because screen coordinates are in pixels, we need to switch to double for movement calculations in a vector space. When rendering on the screen, we simply round the values to integers to convert them to pixel coordinates.
The velocities we will use are as follows:
-
Linear Velocity: The directional vector whose magnitude (length of the vector) represents the speed at which the object will move, measured in pixels per second or per frame. -
Angular Velocity: The rate of change of the orientation angle, as turning takes time and is not instantaneous. This represents the speed at which the orientation angle changes, measured in radians per second or per frame.
double AngularVelocity {};
double LinearVelocity {};
To update the positions of objects in our physics system, we start with the orientation angle. We update the orientation angle by incrementing it with the value obtained from the angular velocity:
aPhy.angle += aPhy.AngularVelocity;
For our implementation, we want the angle to have a maximum value of \( 2PI \). Therefore, we need to ensure that if the angle exceeds this maximum value during increment, it is reset to \( 2PI \).
aPhy.angle += aPhy.AngularVelocity;
if (aPhy.angle > 2.0 * std::numbers::pi) aPhy.angle -= 2.0 * std::numbers::pi;
if (aPhy.angle < 0.0) aPhy.angle += 2.0 * std::numbers::pi;
In coordinate systems like the one used with Raylib, the origin (0,0) is at the top-left corner, so the positive y-axis points downward. As a result, positive rotation is clockwise. Typically, in most coordinate systems, positive rotation is counterclockwise.
With the updated orientation angle, we can calculate the projections on the \( X \) and \( Y \) axes using the trigonometric functions sine and cosine. These projections represent the new location of the object. By multiplying these values by the linear velocity, we obtain the velocity vector coordinates.
// Update velocity
aPhy.vx = aPhy.LinearVelocity * std::cos(aPhy.angle);
aPhy.vy = aPhy.LinearVelocity * std::sin(aPhy.angle);
Finally, with the velocity vector coordinates, we can update the object's position as follows:
//Update position
aPhy.x += phy.vx;
aPhy.y += phy.vy;
With this code, we are working in pixels per frame, but we need it to be dependent on the elapsed time in seconds. That's why we use delta time in game loops, which represents the amount of time that has passed since the last iteration. This ensures that all calculations account for this unit of time and everything is based on seconds.
We calculate the elapsed time and pass it as an argument through each update of the loop, ensuring that all movement calculations are relative to what should occur in one second.
// Angle based on seconds
aPhy.angle += dt * aPhy.AngularVelocity;
// Position based on seconds
aPhy.x += dt * aPhy.vx;
aPhy.y += dt * aPhy.vy;
Now, the linear and angular velocities are relative to one second instead of a single frame. Therefore, we need to subdivide the velocities by 60 to ensure that in each frame, the movement is \( 1/60th \) of the total, corresponding to the time elapsed since the timer last started.
Thus, we multiply both velocities by delta time to make them proportional to the time elapsed in a frame. The updated code would look like this:
void PhysicsSystem::UpdateEntity(PhysicsComponent& aPhy, const bool dt)
{
aPhy.angle += dt * aPhy.AngularVelocity;
if (aPhy.angle > 2.0 * std::numbers::pi) aPhy.angle -= 2.0 * std::numbers::pi;
if (aPhy.angle < 0.0) aPhy.angle += 2.0 * std::numbers::pi;
aPhy.vx = aPhy.LinearVelocity * std::cos(aPhy.angle);
aPhy.vy = aPhy.LinearVelocity * std::sin(aPhy.angle);
aPhy.x += dt * aPhy.vx;
aPhy.y += dt * aPhy.vy;
}
Remember that with this transformation to seconds, we need to adjust the velocities set in the input since they were originally intended for pixels per frame.
Regarding the number of updates per second, updating the physics system around 10 times is more than enough. This leaves the rendering system free to update as frequently as desired.
AI Movement
Once we know how to update positions using linear and angular velocities through kinematic movement, the next step is to implement how the AI will calculate these velocities.
First and foremost, we need to reset the velocity values to zero; otherwise, we would accumulate values with each frame, which would be incorrect.
aPhy.LinearVelocity = 0;
aPhy.AngularVelocity = 0;
Given the AI's position and the position of a target to follow, the first step is to calculate the distance vector between these two points.
This is done by subtracting the coordinates of the target from the coordinates of the AI for each axis. Using the Pythagorean theorem, we can then determine the magnitude of this vector to find the distance between the two points.
auto vtx {aAI.TargetX - aPhy.x};
auto vty {aAI.TargetY - aPhy.y};
auto LinearDistance {std::sqrt(vtx*vtx + vty*vty)};
We can define an epsilon constant as a variable to signify the arrival at the target. Since we are dealing with decimal values, the precision is very high, and it is possible that we may never reach exactly zero.
if (LinearDistance < aPhy.kEpsilon)
{
aAI.TargetActive = false;
std::printf("AI has arrived!\n");
return;
}
If the target has not been reached, we continue with the calculations. In this scenario, we would already have the linear velocity. Since it is based on the distance, the farther away the target is, the higher the linear velocity will be.
Therefore, we will clamp this value between a maximum and minimum that we have set.
aPhy.LinearVelocity = std::clamp(LinearDistance,
-aPhy.kMaxLinearVelocity, aPhy.kMaxLinearVelocity);
To calculate the angular velocity, we first need to determine the target angle. Given the projections of each axis of the distance between the two points, we can find the tangent, as it is a ratio between the sine and cosine. Since the tangent is a ratio, the radius factor is the same on both sides of the division, making the tangent consistent regardless of the distance.
With this in mind, we can use the trigonometric formula for the arc-tangent, which represents the angle for a given tangent and remains the same regardless of the distance between the two points.
The C++ library cmath provides the atan2 function, which allows us to obtain the angle from the sine and cosine values.
auto TargetAngle {std::atan2(vty, vtx)};
One important consideration is the issue with the tangent function when it is parallel to the X-axis, such as when the angle is π/2, because its length becomes infinite. This makes sense mathematically since this occurs when the cosine of the angle is zero, causing the division to yield infinity.
The C++ cmath library takes it into account for this scenario, and instead of returning infinity when the tangent is parallel to the X-axis, it returns π/2.
In addition, the atan2 function assumes one side is positive and the other negative. Therefore, if the resulting angle is greater than π, the atan2 function mirrors the first two quadrants.
As a result, when it reaches 180 degrees, it starts decrementing from -180 back to 0.
Since our implementation works with positive angles from 0 to 2π, we convert to positive as follows:
auto TargetAngle {std::atan2(vty, vtx)};
if (TargetAngle < 0) TargetAngle += 2 * std::numbers::pi;
Thus, if the angular distance between the target angle and the current AI angle is greater than \( PI \), it would be faster to rotate in the opposite direction. Therefore, we will use the complementary angle as the angular velocity in such cases.
auto AngularDistance {TargetAngle - aPhy.angle};
if (AngularDistance > std::numbers::pi) AngularDistance -= 2 * std::numbers::pi;
else if (AngularDistance < -std::numbers::pi) AngularDistance += 2 * std::numbers::pi;
Finally, we clamp the value of the angular distance within a predefined minimum and maximum range.
aPhy.AngularVelocity = std::clamp(AngularDistance,
-aPhy->kMaxAngularVelocity, aPhy->kMaxAngularVelocity);
The complete code we would have is as follows:
void AISystem::UpdateEntity(AIComponent& aAI, PhysicsComponent& aPhy)
{
if (!aAI.TargetActive) return;
aPhy.LinearVelocity = 0;
aPhy.AngularVelocity = 0;
auto vtx {aAI.TargetX - aPhy.x};
auto vty {aAI.TargetY - aPhy.y};
auto LinearDistance {std::sqrt(vtx*vtx + vty*vty)};
if (LinearDistance < aPhy.kEpsilon)
{
aAI.TargetActive = false;
std::printf("AI has arrived!\n");
return;
}
aPhy.LinearVelocity = std::clamp(LinearDistance,
-aPhy.kMaxLinearVelocity, aPhy.kMaxLinearVelocity);
auto TargetAngle {std::atan2(vty, vtx)};
if (TargetAngle < 0) TargetAngle += 2 * std::numbers::pi;
auto AngularDistance {TargetAngle - aPhy.angle};
if (AngularDistance > std::numbers::pi) AngularDistance -= 2 * std::numbers::pi;
else if (AngularDistance < -std::numbers::pi) AngularDistance += 2 * std::numbers::pi;
aPhy.AngularVelocity = std::clamp(AngularDistance,
-aPhy->kMaxAngularVelocity, aPhy->kMaxAngularVelocity);
}
Dynamic Movement
In dynamic movement, accelerations are introduced. Previously, from a target position, we determined the velocities needed to reach that target. Now, we need to do the same with velocities, deriving accelerations to achieve those target velocities.
With accelerations, the speed of characters will not change instantly (e.g., from 0 to 100 in a single frame) but will increase gradually. The same principle applies when slowing down. This concept forms the basis of dynamic movements.
To achieve dynamic vectorial movement, both player input and AI need to modify accelerations instead of velocities.
-
Linear Acceleration: Pixels per second squared, meaning how many pixels the linear velocity increases in one second. -
Angular Acceleration: Radians per second squared, meaning how many radians the angular velocity increases in one second.
double LinearAcceleration {};
double AngularAcceleration {};
We can make it dependent on the final speed, allowing us to decide how many seconds it will take to reach the target linear velocity. In our case, the target linear velocity will be achieved in 2 seconds.
static constexpr double kMaxLinearVelocity { 100.0 };
static constexpr double kMaxLinearAcceleration { kMaxLinearVelocity / 2.0 };
static constexpr double kMaxAngularVelocity { 3 * std::numbers::pi };
static constexpr double kMaxAngularAcceleration { kMaxAngularVelocity / 2.0 };
In our player input code, we would replace the modification of velocities with accelerations.
aPhy.LinearAcceleration = 0;
aPhy.AngularVelocity = 0;
if (Input::KeyPressed( aInput.UP)) aPhy.LinearAcceleration = aPhy->kMaxLinearAcceleration;
if (Input::KeyPressed(aInput.DOWN)) aPhy.LinearAcceleration = -aPhy->kMaxLinearAcceleration;
if (Input::KeyPressed( aInput.LEFT)) aPhy.AngularVelocity = -aPhy->kMaxAngularVelocity;
if (Input::KeyPressed(aInput.RIGHT)) aPhy.AngularVelocity = aPhy->kMaxAngularVelocity;
While the angular acceleration variable is included, it is generally not recommended to use it due to the potential for erratic behavior. If you are rotating in one direction and want to switch to the opposite direction, you would first need to decelerate and then accelerate in the new direction. In our implementation, we will discard this approach and only allow acceleration in the direction we are facing.
Newton Euler 1 Integration
Based on Newton's equation of uniformly accelerated motion, we analyze the time:
From the perspective of our application, \( t \) represents the time elapsed between each iteration of the game loop, so the differential of \( t \) will be \( 1/60 \). If we square it, it's equivalent to \( 1/(60*60) = 1/3600 \). Additionally, if we divide the acceleration by two, we get a time of \( 1/7200 \) which is then multiplied by the acceleration.
This value is ridiculously small and practically negligible, wasting CPU cycles in the calculation. ecause this value is so insignificant, the Newtonian equation is not typically used in dynamic movements.
Instead, what is known as Newton-Euler 1 Integration, is used.
This approach is simpler but highly effective and provides results that are very close to the actual values.
Our physics code would be updated as follows with the addition of accelerations:
// Updating position by velocity calculations...
//// Updating velocity by acceleration calculations
aPhy.LinearVelocity += dt * aPhy.LinearAcceleration;
aPhy.AngularVelocity += dt * aPhy.AngularAcceleration;
aPhy.LinearVelocity = std::clamp(aPhy.LinearVelocity,
-aPhy.kMaxLinearVelocity, aPhy.kMaxLinearVelocity);
aPhy.AngularVelocity = std::clamp(aPhy.AngularVelocity,
-aPhy.kMaxAngularVelocity, aPhy.kMaxAngularVelocity);
AI Movement
For calculating accelerations in our AI, as we said before, we will update just the part that involves the linear acceleration, as the rotation will prevail the same.
First of all, we need to reset their values to zero at the start of each frame. We then compute the difference between the target linear velocity, determined from the distance to our target, and our current linear velocity.
Finally, we clamp the resulting acceleration value within the established limits.
// Reset accelerations
aPhy.LinearAcceleration = 0;
aPhy.AngularVelocity = 0;
// Clamp linear distance to get the target velocity
auto TargetVelocity {std::clamp(LinearDistance,
-aPhy.kMaxLinearVelocity, aPhy.kMaxLinearVelocity)};
// Calculate the acceleration
auto Acceleration {TargetVelocity - aPhy.LinearVelocity};
// Clamp and set the linear acceleration
aPhy.LinearAcceleration = std::clamp(Acceleration,
-phy->kMaxLinearAcceleration, phy->kMaxLinearAcceleration);
AI Parametrization
From a gameplay perspective, it is crucial to breathe life and personality into our AI. To achieve this, we introduce the following parameters to create diverse behaviors for each unit:
Arrival Radius: We transform the previously constant epsilon into a variable, allowing us to customize the behavior of each AI unit, giving them unique personalities.
double ArrivalRadius { 1.0 }; // pixel unit
if (LinearDistance < AI.ArrivalRadius)
{
AI.TargetActive = false;
std::printf("[%lld] AI has arrived!\n", Entity->GetEntityID());
return;
}
Time to Arrive: This controls the time it takes for a unit to reach its target, ensuring that the distance decreases not linearly as it approaches but relative to the time. Previously, the distance was designed to be covered in one second. Now, we make the linear velocity proportional to the desired travel time. We don't need to worry about the unit moving too fast since it's clamped to a maximum speed.
This parameter allows us to customize how quickly a unit can reach its target, adding more personality to the AI.
double Time2Arrive { 0.5 }; // seconds
// Calculate Linear velocity based on time to arrive
aPhy.LinearVelocity = std::clamp(LinearDistance / AI.Time2Arrive ,
-aPhy.kMaxLinearVelocity, aPhy.kMaxLinearVelocity);
// Angular velocity based on time to arrive
aPhy.AngularVelocity = std::clamp(AngularDistance / AI.Time2Arrive,
-aPhy.kMaxAngularVelocity, aPhy.kMaxAngularVelocity);
This with the calculation of linear acceleration, it would be as follows:
// Linear acceleration based on time to arrive
auto TargetVelocity { std::clamp(LinearDistance / AI.Time2Arrive,
-aPhy.kMaxLinearVelocity, aPhy.kMaxLinearVelocity) };
aPhy.LinearAcceleration = std::clamp((TargetVelocity - aPhy.LinearVelocity) / AI.Time2Arrive,
-aPhy.kMaxLinearAcceleration, aPhy.kMaxLinearAcceleration);
// Angular velocity based on time to arrive
phy->AngularVelocity = std::clamp(AngularDistance / AI.Time2Arrive,
-phy->kMaxAngularVelocity, phy->kMaxAngularVelocity);
Drag
The drag coefficient represents the proportion of velocity lost in one second. For instance, a drag of 0.95 means that 95% of the velocity will be lost in one second, leaving only 5% of the original speed.
static constexpr double kDrag { 0.95 }; // 95% velocity loss
We could also use this concept as a parameter to make the AI more slippery or harder to move depending on the terrain type. The calculation of the new linear velocity with the applied drag would be added to our physics as follows.
// Physics calculations...
// Drag calculation
auto Drag {dt * std::fabs(aPhy.LinearVelocity) * aPhy.kDrag};
if (phy.LinearVelocity > 0) phy.LinearVelocity -= Drag;
else phy.LinearVelocity += Drag;
Be cautious with the drag value. If it exceeds 1, the subtraction might result in a negative value, causing unintended backward movement. However, this shouldn't occur since we always subtract a proportion of the current velocity.
Steering Behaviors
To parameterize behaviors in our entities, we define a set of known behaviors called steering behaviors.
Each steering behavior is encapsulated in global functions to remain independent of the AI system, allowing them to be used in various parts of the code as needed. These functions return an output in the form of a steering structure, which holds the accelerations calculated by the behavior.
This structure can be seen as follows:
struct Steer_t
{
double linear {0.0};
double angular {0.0};
};
The procedure for managing these behaviors is currently handled within the AI system. A switch statement is used to select the appropriate behavior, calculate the necessary accelerations, and store them in the AI's physics component.
Phy->LinearAcceleration = phy->AngularVelocity = 0;
if (!AI->TargetActive) return;
Steer Steering {};
auto TargetPos {Point2D{AI.TargetX, AI.TargetY}};
switch (AI.Behaviour)
{
case SB::Arrive: Steering = steerings::Arrive(*Phy, TargetPos, AI.ArrivalRadius, AI.Time2Arrive); break;
case SB::Seek: Steering = steerings::Seek (*Phy, TargetPos, AI.Time2Arrive); break;
case SB::Flee: Steering = steerings::Flee (*Phy, TargetPos, AI.Time2Arrive); break;
}
Phy->LinearAcceleration = Steering.Linear;
Phy->AngularVelocity = Steering.Angular;
Arrive
Arrive is the most basic steering behavior. It targets a specific point and moves towards it until it reaches the location, at which point the behavior terminates.
By encapsulating all the AI logic explained so far into a global function, we achieve the Arrive behavior:
constexpr Steer
Arrive(PhysicsComponent& aPhy, const Point2D& aTarget, const double aArrivalRadius,
const double aTime2Arrive) const
{
Steer st {};
// Linear distance to target
auto vtx { aTarget.x - aPhy.x };
auto vty { aTarget.y - aPhy.y };
auto LinearDistance { std::sqrt(vtx*vtx + vty*vty) };
// If radius threshold is reached, we exit the behavior.
if (LinearDistance < aArrivalRadius) return {};
// Set linear acceleration
auto TargetVelocity {std::clamp(LinearDistance / aTime2Arrive ,
-phy.kMaxLinearVelocity, phy.kMaxLinearVelocity)};
st.Linear = std::clamp( (TargetVelocity - aPhy.LinearVelocity) / aTime2Arrive,
-phy.kMaxLinAcceleration, phy.kMaxLinAcceleration);
// Set angular velocity
auto TargetAngle {std::atan2(vty, vtx)};
if ( TargetAngle < 0.0 ) TargetAngle += 2.0 * std::numbers::pi;
auto AngularDistance { TargetAngle - aPhy.angle };
if (AngularDistance > std::numbers::pi) AngularDistance -= 2 * std::numbers::pi;
else if (AngularDistance < -std::numbers::pi) AngularDistance += 2 * std::numbers::pi;
st.Angular = std::clamp(AngularDistance / aTime2Arrive,
-aPhy.kMaxAngularVelocity, aPhy.kMaxAngularVelocity);
return st;
}
Seek
The seek behavior differs from the arrive behavior in that it continuously follows the target and does not conclude upon reaching its position. Additionally, seek behavior requires moving at maximum linear velocity without the need to accelerate to reach that speed.
The issue arises when the entity's orientation differs from the target's orientation, causing a parabolic movement due to simultaneous movement and rotation.
To mitigate this, the seek behavior will aim to align with the target as quickly as possible and will accelerate more when it is better aligned with the target. Thus, the AI's acceleration will be weighted based on how well it is oriented towards the target.
To achieve this, we can add a proportion relative to the maximum linear velocity. When the entity is aligned with the target, its angular orientation difference is zero, allowing it to move at maximum speed. However, if the orientation is not aligned, we divide the maximum velocity by the angular difference to reduce the speed accordingly. It is important to note that the angular velocity should be taken as an absolute value since it can be negative, and a negative denominator could lead to incorrect calculations as we could divide by zero!
auto AngularVelSize { std::fabs(AngularVelocity) };
auto LinearAcceleration { aPhy.kMaxLinearVelocity / (1 + AngularVelSize) };
aPhy.LinearAcceleration = std::clamp( LinearAcceleration / AI.Time2Arrive,
-phy.kMaxLinearAcceleration, phy.kMaxLinearAcceleration);
This approach ensures that the entity prioritizes turning first and then moves towards the target once it is aligned.
By encapsulating this AI logic within a global function, we can achieve the seek behavior.
constexpr Steer
Seek(PhysicsComponent const& aPhy, const Point2D& aTarget, const double Time2Arrive)
{
Steer st {};
// Linear distance to target
auto vtx { aTarget.x - aPhy.x };
auto vty { aTarget.y - aPhy.y };
auto TargetDistance { std::sqrt(vtx*vtx + vty*vty) };
// Target Orientation
auto TargetOrientation { std::atan2(vty, vtx) };
if ( TargetOrientation < 0.0 ) TargetOrientation += (2.0 * std::numbers::pi);
// Target angular velocity
auto AngularDistance { TargetOrientation - aPhy.angle };
if (AngularDistance > std::numbers::pi) AngularDistance -= 2 * std::numbers::pi;
else if (AngularDistance < -std::numbers::pi) AngularDistance += 2 * std::numbers::pi;
// Set angular velocity
auto AngularVelocity { AngularDistance / Time2Arrive };
st.Angular = std::clamp(AngularVelocity, -phy.kMaxVAng, phy.kMaxVAng);
// Set linear velocity based on max velocity proportion
auto AngularVelSize { std::fabs(AngularVelocity) };
auto LinearAcceleration { aPhy.kMaxLinearVelocity / (1 + AngularVelSize) };
st.Linear = std::clamp( LinearAcceleration / Time2Arrive,
-phy.kMaxLinearAcceleration, phy.kMaxLinearAcceleration);
return st;
}
Flee
Once the seek behavior is understood, implementing the flee behavior becomes straightforward. The flee behavior is essentially the seek behavior but directed away from the target.
To achieve this, we calculate the direction vector from the AI to the target and then invert it to point in the opposite direction. By multiplying this vector by 2, we can determine the position directly opposite the target.
Encapsulating this logic within a global function, we can efficiently implement the flee behavior.
Steer
Flee(PhysicsComponent const& aPhy, Point2D const& aFleePos, double const aTime2Flee)
{
Point2D_t Target { 2 * aPhy.x - aFleePos.x, 2 * aPhy.y - aFleePos.y};
return Seek(aPhy, Target, aTime2Flee);
}
Pursue
The Pursue behavior is more advanced as it not only follows the target continuously but also predicts the target's future position at each second. This allows the AI to anticipate where the target is heading and intercept it along the way.
To achieve this behavior, we need to calculate the distance between the AI and the target, determine the minimum time it would take for the AI to cover that distance at its maximum linear speed, and use the Newtonian equation of rectilinear motion to predict the target's future position based on its current velocity and position. Then, the time it takes for the AI to reach it.
This requires access to the target's physics data, including its current speed and position.
By encapsulating this AI logic into a global function, we can implement the Pursue behavior effectively.
constexpr Steer
Pursue(PhysicsComponent const& aPhyTarget, PhysicsComponent const& aPhyPursuer,
double const aTime2Arrive)
{
// Linear distance to target
auto vtx { aPhyTarget.x - aPhyPursuer.x };
auto vty { aPhyTarget.y - aPhyPursuer.y };
auto TargetDistance { std::sqrt(vtx*vtx + vty*vty) };
// Minimum time to reach target from max velocity (x = v * t)
auto DistanceTime { TargetDistance / aPhyPursuer.kMaxLinearVelocity };
// Calculate predicted target position based on distance time (xf = x0 + v * t)
Point2D PredictedTarget
{
aPhyTarget.x + aPhyTarget.vx * DistanceTime,
aPhyTarget.y + aPhyTarget.vy * DistanceTime
};
return Seek(aPhyPursuer, PredictedTarget, aTime2Arrive);
}
Evade
The Evade steering behavior functions similarly to the Pursue behavior, but instead of moving towards the predicted position, it moves in the opposite direction of the predicted position. This makes it a more advanced version of the Flee behavior.
constexpr Steer
Evade(PhysicsComponent const& aPhyTarget, PhysicsComponent const& aPhyPursuer,
double const aTime2Arrive)
{
// Linear distance to target
auto vtx { aPhyTarget.x - aPhyPursuer.x };
auto vty { aPhyTarget.y - aPhyPursuer.y };
auto TargetDistance { std::sqrt(vtx*vtx + vty*vty) };
// Minimum time to reach target from max velocity (x = v * t)
auto DistanceTime { TargetDistance / aPhyPursuer.kMaxLinearVelocity };
// Calculate predicted target position based on distance time (xf = x0 + v * t)
Point2D PredictedTarget
{
aPhyTarget.x + aPhyTarget.vx * DistanceTime,
aPhyTarget.y + aPhyTarget.vy * DistanceTime
};
return Flee(aPhyPursuer, PredictedTarget, aTime2Arrive);
}
Follow
The Follow behavior, or Path Following, involves the AI moving between various locations known as waypoints, thereby creating a path.
To implement this, we can reuse the arrive behavior by providing it with an array of waypoints. When the AI reaches a waypoint and the accelerations reach zero, indicating it has arrived, we increment the iterator to move on to the next destination in the path.
constexpr Steer
Follow(PhysicsComponent const& aPhy, auto& aPathIter, double const aArrivalRadius,
double const aTime2Arrive)
{
auto St {Arrive(aPhy, *aPathIter, aArrivalRadius, aTime2Arrive)};
// If radius threshold is reached, we can move on to the next waypoint
if (St == Steer{})
{
++aPathIter;
}
return St;
}
To implement this behavior, a custom iterator was developed that resets to the first element of the container once it surpasses the end of the array, thereby restarting the behavior.
AI Tech & Techniques
Artificial intelligence not only focuses on behaviors and mathematical equations to produce the desired movement but also encompasses various technologies and software techniques used in the game AI. These contribute to creating more robust, flexible, and maintainable code that can be easily extended over time.
Blackboard Architecture
Blackboard architectures rely on a shared board among entities in the world, which contains global information such as the target destination for entities, designed paths, level information, and more.
Therefore, the blackboard represents a component where all entities can read from and write to. There should only be a single instance of the blackboard component, making it similar in design to a singleton.
One recommendation when implementing these types of components is to define a tuple as a data structure to collect different types of singleton components based on the desired logic separation: Blackboard, LevelData, AIData, SceneData, etc.
Example of a Blackboard component, where entities would read the shared objective or the type of behavior they need to execute:
struct CBlackboardComponent
{
double TargetX {0.0}, TargetY {0.0};
eBehaviourType Behaviour { eBehaviourType::Seek };
bool TargetActive { false };
};
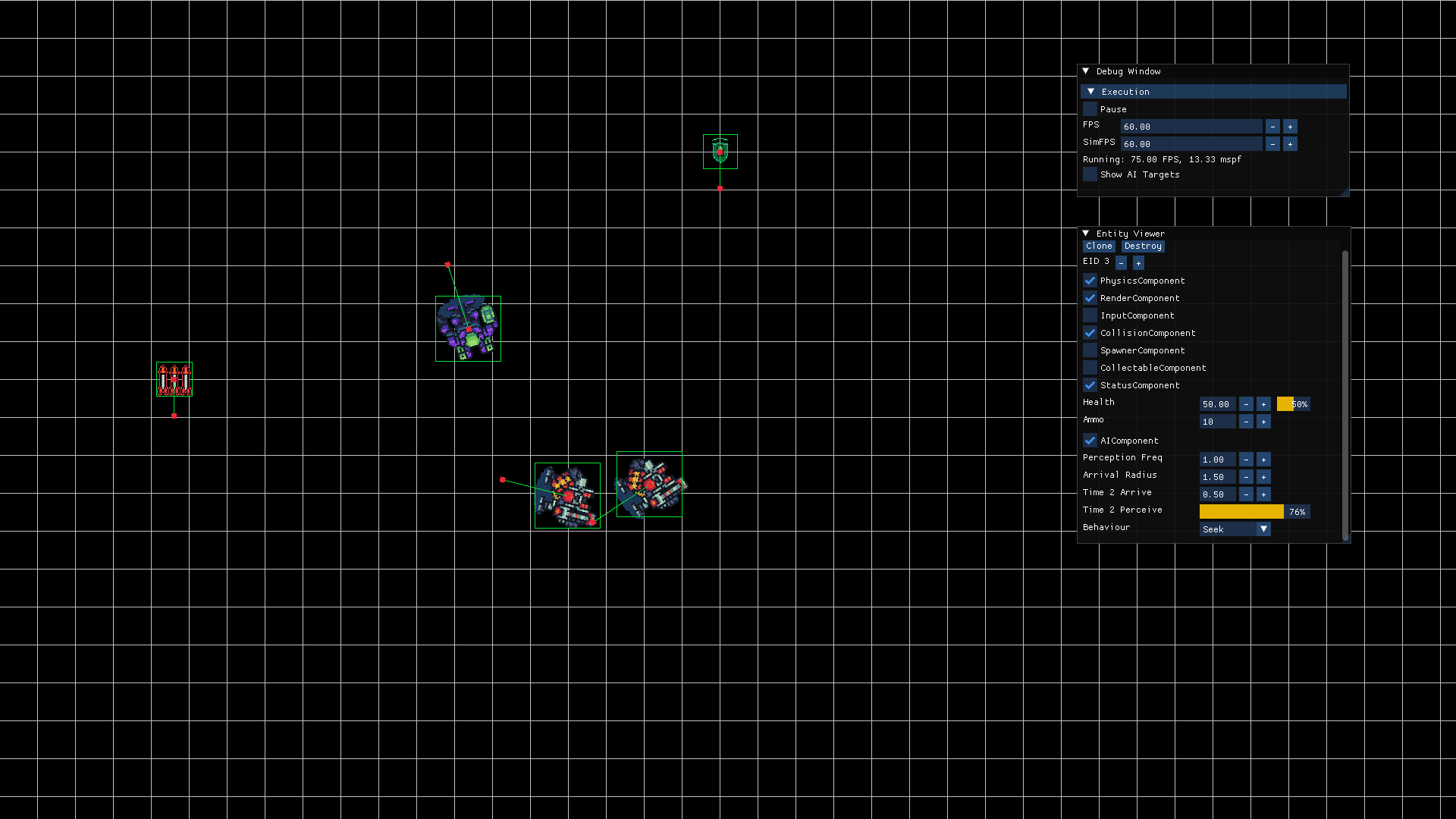
Perception
If we run the behaviors implemented in our AI, we will notice that the AI's response to pursuing the target is instantaneous, with no reaction time. The AI immediately reacts to the player's input events.
In the real world, when we are following a target and it changes direction, there is a specific reaction time before we decide to change direction as well. To achieve a more realistic outcome, AI systems should mimic this behavior by incorporating a response time to the player's movements.
It is as simple as reducing the frequency at which the AI system updates to check what behavior it should perform. Having the AI make 60 different decisions in one second is unnatural, so it should not perceive updates that frequently.
A human reaction would be equivalent to pressing between 10 and 12 keys per second at most. Therefore, we could define a variable representing this frequency. If the frequency is 10, the time we have for each perception is 1/10.
// Perception time (cooldown)
// --------------------------
double mPerceptionTime { 0.1 }; // Freq inverse -> 10 times per second = 1 / 10 perception time
double mAccumulatedTime { 0.0 };
In the future, we can adjust the response time frequency to simulate different states such as fatigue, poisoning, or drunkenness in the AI.
Here we have an implementation where we are accumulating a counter from the delta time factor and when the value reach perception time, we reset the accumulated delta time and perceive in order to execute the behaviors.
AI.mAccumulatedTime += dt;
if (AI.mAccumulatedTime <= AI.mPerceptionTime) return;
// Perception Time reached
// -----------------------
AI.mAccumulatedTime -= AI.mPerceptionTime;
// Perceive individual or shared AI behaviors...
// ---------------------------------------------
Decoupled Systems
As we have seen in the code examples, there is a lot of repeated code in AI behaviors, which makes the code "smelly." In software development, we need to conceptualize the code to reuse it in different parts, modularize it away from other concepts, and ensure that any modifications to one part automatically update all related parts. This approach results in more robust and maintainable code.
To make AI behaviors reusable, it's also important that they are not tightly coupled to specific data types and the ECS (Entity Component System) framework. Forcing them to depend on these specifics would limit their use in other contexts.
AI behavior methods should perform the necessary calculations and return the results as velocities and accelerations—data that are independent of the engine and ECS framework. This way, the methods can be used in any other application.
The ideal scenario is to decouple these behaviors from any specific components so they only take raw parameters, recognizable by any application, to perform their calculations and produce a response. These methods should not modify or interact with anything related to the game or engine, ensuring they remain decoupled from the systems.
Therefore, we have created a data structure designed to be returned by these behavior methods with the necessary data for operations. This data is then stored in the physics component to calculate the final positions.
struct Steer
{
double Linear {0.0};
double Angular {0.0};
};
Content Creation Tools
To improve our AI systems, it is essential to add debugging tools that allow us to iterate and modify parameters in real-time, enabling immediate observation of results. This will significantly reduce development time and enhance the polish of our games.
One of the most important debugging parameters is the ability to control the application's frame rate, allowing us to monitor what is happening in the scene.
For our debugging tool, we define two types of frame rates:
-
Render Frame Rate: The number of times we update in relation to the screen refresh rate or free update. We want the render and input systems to update based on this frame rate. -
Simulation Frame Rate: The number of times we update the world per second. This is separate from the render frame rate because we want the render and input systems to update continuously, while physics and AI only need to update a certain number of times per second, as they do not need to be updated every frame.
For example, we would have a frame rate that updates based on the screen refresh rate at 75 frames per second, and another frame rate that updates at 60 frames per second for world simulation.
uint64_t Nanos { static_cast< uint64_t >(1000000000 / Dbg.FPS) }; // 16ms in nanos
Render.Update( ECSManager );
Input.Update( ECSManager );
if (Dbg.Timer.Ellapsed() > Nanos)
{
AI.Update(ECSManager, 1 / Dbg.FPS );
Physics.Update( ECSManager, 1 / Dbg.FPS );
Dbg.Timer.Start();
}
On one hand, we have the frames the application uses to render in a second, and on the other, we have the frames the application sets to update the simulation. We might want to render at 1 frame per second while simulating at 60 frames per second. This allows us to observe the simulation more slowly, ensuring we don't miss any details of what happens in one second.
To achieve this, we define a new debug variable for simulation stepping or delta time. This allows us to differentiate between how many frames per second the simulation updates and the number of simulation steps executed, as well as the duration of each step.
Each frame we update represents of the simulation time. Therefore, we still need 60 frames to simulate one second of execution, but we will see it expanded over time.
We can understand this new concept in the following code adding a new variable for the simulation step time.
uint64_t Nanos { static_cast< uint64_t >(1000000000 / Dbg.FPS) }; // 16ms in nanos
Render.Update( ECSManager );
Input.Update( ECSManager );
if (Dbg.Timer.Ellapsed() > Nanos)
{
auto SimDT { 1.0 / dbg.SimFPS };
AI.Update(ECSManager, SimDT );
Physics.Update( ECSManager, SimDT );
Dbg.Timer.Start();
}
Now we can lower the FPS without affecting the simulation. The simulation still runs at 60 steps per second, so I can observe it in detail without impacting the overall simulation.
By adjusting the simulated FPS values, we can control the time steps of the simulation, allowing us to simulate more time with fewer frames or less time with more frames.
Additionally, we can add the functionality to pause the world simulation, enabling us to pause the simulation without impacting the rest of the system.
uint64_t Nanos { static_cast< uint64_t >(1000000000 / Dbg.FPS) }; // 16ms in nanos
Render.Update( ECSManager );
Input.Update( ECSManager );
if ((!Dbg.Pause.Value) && (Dbg.Timer.Ellapsed() > Nanos))
{
auto SimDT { 1.0 / dbg.SimFPS };
AI.Update(ECSManager, SimDT );
Physics.Update( ECSManager, SimDT );
Dbg.Timer.Start();
}
Decision Making
In Game AI, decision making is the ability of a character to decide what to do. Carrying out that decision (movement, animation, etc) is taken for granted. Most games use very simple decision making systems as state machines, decision trees, rule-based systems etc.
In this chapter, we will explore some of the most important decision making tools, from the simplest to the most sophisticated ones.
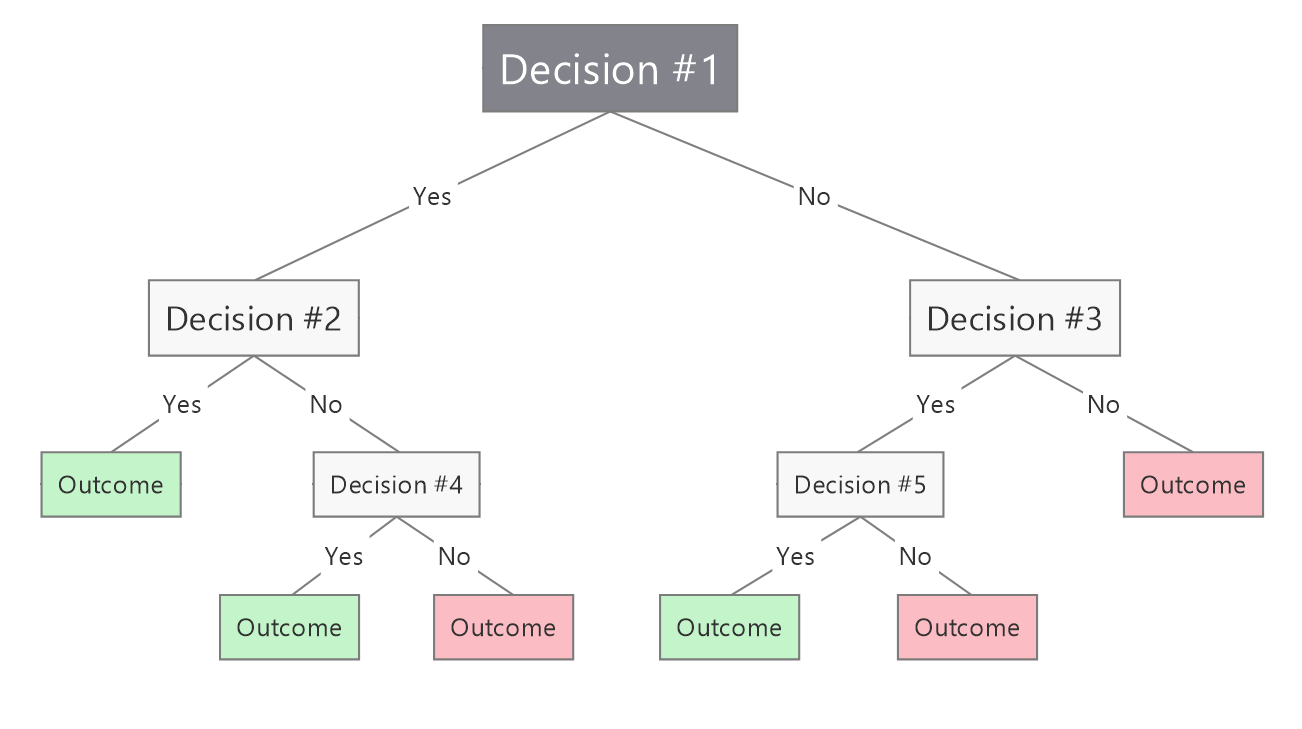
Decision Trees
Decision trees are one of the simplest structures for AI decision-making in video games. Their simplicity and versatility make them widely used in most games, as more advanced and sophisticated methods are often unnecessary. However, a more refined and modern version, known as behavior trees, is now commonly used.
Trees are data structures that often get distributed across memory in a fragmented manner. If we don't manage this data distribution effectively, it can lead to significant performance drawbacks and slower memory access speeds. Therefore, it is crucial to optimize trees for cache efficiency and linear memory access.
In a decision tree composed of actions, these actions are not atomic, meaning they do not occur in every frame. It does not make sense to decide to do action A in frame 1 and then switch to action B in the next frame. Actions should last for a certain duration.
Nodes
It is crucial to treat these actions as data, allowing designers the flexibility to modify them and change the AI's behavior and logic, preferably in real-time and saved from an external file. Otherwise, if they are treated as code, each change or modification would require adding new code and recompiling the application to test the change. Over time, this approach can lead to convoluted code with difficult-to-understand and maintain conditional statements.
To represent each of these actions in memory, we use the concept of a node. A node is essentially a structure containing data for each action, including its internal data and references to other nodes that should be executed when certain conditions are met. Therefore, each node can have child nodes. Besides storing data, nodes can also have member functions to process this data.
We can have various types of nodes, such as action nodes, decision nodes, etc. Each type will perform a different task, but they will all be treated and processed in the same way. To achieve this, we will utilize the polymorphism provided by C++, allowing us to execute different behaviors treated as the same way.
Let's see an approximation of a basic node interface class implementation.
In our implementation, we want to avoid accidental copying of nodes. Therefore, we will remove the copy constructors and assignment operators from their class for now.
struct CDecisionNode
{
CDecisionNode() = default;
virtual ~CDecisionNode() = default;
CDecisionNode(const CDecisionNode&) = delete;
CDecisionNode(CDecisionNode&&) = delete;
CDecisionNode& operator=(const CDecisionNode&) = delete;
CDecisionNode& operator=(CDecisionNode&&) = delete;
virtual void Run(WorldContext& aContext) noexcept = 0;
};
Node Tree
The tree should never manage resources, only use them. Managing resources within the tree can complicate code maintenance significantly, as multiple nodes might point to the same child node. This would require careful consideration of the child node's lifespan to prevent it from being destroyed by any of its referencing parent nodes.
If we instantiate each node on the heap and store it in a container, traversing that container will disrupt cache performance. This is because accessing the nodes causes memory jumps, which significantly degrades cache efficiency. Cache optimization can improve processing times by up to a factor of 200 to 1, so maintaining contiguous memory access is crucial for performance.
Therefore, we need to implement a tree that allocates nodes in a contiguous and orderly manner in memory.
Additionally, the tree will require a reference to the world simulation, as the nodes will need information about the player's position, other AI units, and more. We need not only information about our internal state but also about the world around us.
This would be a basic implementation of a decision tree, with its vector of unique_ptr as the container of nodes, which are processed in the run() method.
struct CDecisionTree
{
using value_type = std::unique_ptr< BTNode_t >;
using NodeStorage = std::vector< value_type >;
explicit CDecisionTree() = default;
void Run(WorldContext& aContext) noexcept
{
if (!mNodes.empty())
{
mNodes.back()->Run(aContext);
}
}
private:
NodeStorage mNodes {};
};
Cache and Optimization
We must consider that the new operation in C++ is one of the most expensive operations. This is because it involves a call to the operating system, which runs through a privilege scale. We have to wait in line until the operating system processes our request, executes privileged code, reserves the memory page (4KB) in the heap, and returns it to us. This entire procedure makes it an extremely slow operation.
The next new calls will use the reserved memory page until it is filled; however, they should never be performed during the game execution cycle as they can cause frame drops.
Another disadvantage of performing these operations is the lack of control over memory allocation. Each time we read a node, we access different memory regions, disrupting the cache.
Let's avoid having each node allocate memory separately and instead decide the memory position for each node ourselves. This way, the tree nodes will have an optimal position for the cache, and each time the tree traverses the nodes, it will do so in a linear and continuous manner.
We must also avoid memory jumps, but if we have to make them, they should be as short as possible because the nodes will be close in memory. Additionally, we should always iterate to the right, never backtracking.
Cache, on the other hand, is not composed of memory pages but rather cache lines, which are filled with data based on a prediction of what will be needed next. In modern processors, these cache lines are typically 64 bytes in size, which is quite small. Most data won't fit into cache lines unless specifically we designed to do so.
In our case, the node tree will not fit entirely within a single cache line and will span multiple lines. However, having the nodes consecutively aligned allows the processor to predict correctly. While processing the initial nodes, it can load the subsequent ones into another cache line. The processor will prefetch the next cache lines, thereby avoiding cache misses.
With more extensive and complex decision trees in game AI, even modern processors may struggle to predict the jump pattern from one node to another, as it can vary greatly depending on the game's circumstances. This could lead to prediction errors, but since the data is read linearly from RAM, the impact will be minimal.
In tree structures, it is common practice to create child nodes first and store them on the right side of the allocated memory. Parent nodes are created last and stored on the left side of the memory.
So, we will store the nodes in a linear and cache-friendly manner primarily to optimize read and write operations during program execution. The creation process is not as critical since it only occurs once at the beginning.
Node Lifetime Management
To implement a tree of nodes stored in a linear and cache-friendly manner, we will use a byte array managed by a unique_ptr to store each node.
using MemoryStorage = std::unique_ptr< std::byte[] >;
std::size_t mMemorySize {1024};
MemoryStorage mMemory {std::make_unique< std::byte[] >(mMemorySize)};
std::byte* pmReserved {mMemory.get() + mMemorySize};
We will use the placement new operator to pass memory addresses from the byte array, allowing us to invoke the constructor of the node object of a specific byte size directly within the array.
In the container holding pointers to the nodes used by the tree, the parent node is the last one. However, in the reserved memory, the parent node is positioned first. This arrangement allows the nodes to be processed from back to front, ensuring they are executed from left to right, which is more cache-friendly.
template < typename NodeType, typename... ParamTypes >
NodeType& CreateNode(ParamTypes&&... aParams)
{
// Reserve memory
// --------------
pmReserved -= sizeof(NodeType);
if (pmReserved < mem.get())
{
pmReserved += sizeof(NodeType);
throw std::bad_alloc{};
}
// Create node
// -----------
auto* pNode = new (pmReserved) NodeType{std::forward< ParamTypes >(aParams)...};
mNodes.emplace_back(pNode);
return *pNode;
}
Therefore, the complete code for the decision tree is as follows:
struct CDecisionTree
{
using value_type = std::unique_ptr< CDecisionNode >;
using NodeStorage = std::vector< value_type >;
using MemoryStorage = std::unique_ptr< std::byte[] >;
explicit CDecisionTree() = default;
void Run(WorldContext& aContext) noexcept
{
if (!mNodes.empty())
{
mNodes.back()->Run(aContext);
}
}
template < typename NodeType, typename... ParamTypes >
NodeType& CreateNode(ParamTypes&&... aParams)
{
// Reserve memory
// --------------
pmReserved -= sizeof(NodeType);
if (pmReserved < mMemory.get())
{
pmReserved += sizeof(NodeType);
throw std::bad_alloc{};
}
// Create node
// -----------
auto* pNode = new (pmReserved) NodeType{std::forward< ParamTypes >(aParams)...};
mNodes.emplace_back(pNode);
return *pNode;
}
private:
std::size_t mMemorySize {1024};
MemoryStorage mMemory {std::make_unique< std::byte[] >(mem_size)};
std::byte* pmReserved {mMemory.get() + mMemorySize};
NodeStorage mNodes {};
};
Since we do not allocate memory for each node object individually, there is no need for any deletion calls. The resources are stored in an array managed by a unique_ptr.
However, as we use a vector of unique_ptrs to manage nodes during the application's execution, these unique_ptrs will attempt to release the resources they manage when the application closes. This should not happen because memory was never allocated for each node individually.
Therefore, we will create a custom deleter for the unique_ptrs that will only call the object's destructor.
struct Deleter
{
void operator()(CDecisionNode* n) { n->~CDecisionNode(); }
};
We can store it within the scope of the Node interface class.
struct CDecisionNode
{
struct Deleter
{
void operator()(CDecisionNode* n) { n->~CDecisionNode(); }
};
CDecisionNode() = default;
virtual ~CDecisionNode() = default;
CDecisionNode(const CDecisionNode&) = delete;
CDecisionNode(CDecisionNode&&) = delete;
CDecisionNode& operator=(const CDecisionNode&) = delete;
CDecisionNode& operator=(CDecisionNode&&) = delete;
virtual void Run(WorldContext& aContext) noexcept = 0;
};
Behavior Trees
Behavior trees are more sophisticated than decision trees. One key difference is that, after executing an action, a behavior tree node returns a result to its parent node to indicate whether the action was successful. This allows the parent node to decide whether to proceed to the next node.
Nodes
With this new key change, two distinctive types of nodes emerge in behavior trees:
-
Sequence Node: This node contains multiple action nodes, which it executes in order. If an action is successful, it moves on to the next one until the sequence is complete. The order is dictated by the actions and their sub-actions. -
Selector Node: This node also contains multiple action nodes, executing them in sequence until one succeeds. As soon as any action returns success, the execution of nodes terminates. The selector establishes a priority order among actions.
States
In addition, behavior trees, each node can return one of three states:
-
Success: The action has been completed. -
Failure: The action has not been completed. -
Running: The action is currently in progress.
We can define an enumerator about them:
enum class eBehaviorNodeStatus : std::uint8_t
{
Success,
Fail,
Running
};
Architecture
Considering the new features provided by behavior trees, the code for the new node interface would be as follows:
struct CBehaviorNode
{
struct Deleter
{
void operator()(CBehaviorNode* aNode) { aNode->~CBehaviorNode(); }
};
CBehaviorNode() = default;
virtual ~CBehaviorNode() = default;
CBehaviorNode(const CBehaviorNode&) = delete;
CBehaviorNode(CBehaviorNode&&) = delete;
CBehaviorNode& operator=(const CBehaviorNode&) = delete;
CBehaviorNode& operator=(CBehaviorNode&&) = delete;
virtual eBehaviorNodeStatus Run(WorldContext& aContext) noexcept = 0;
};
The behavior tree code will also be updated, particularly enhancing the run() method to process nodes by considering the returned results.
template < typename T >
concept BTNodeType = std::derived_from< T, CBehaviorNode >;
struct BehaviourTree
{
using value_type = std::unique_ptr< CBehaviorNode, CBehaviorNode::Deleter >;
using NodeStorage = std::vector< value_type >;
using MemoryStorage = std::unique_ptr< std::byte[] >;
explicit BehaviourTree() = default;
eBehaviorNodeStatus Run(WorldContext& aContext) noexcept
{
if (!mNodes.empty()) return mNodes.back()->Run(aContext);
return eBehaviorNodeStatus::Fail;
}
template < BTNodeType NodeType, typename... ParamTypes >
NodeType& CreateNode(ParamTypes&&... aParams)
{
// Reserve memory
// --------------
pmReserved -= sizeof(NodeType);
if (pmReserved < mMemory.get())
{
pmReserved += sizeof(NodeType);
throw std::bad_alloc{};
}
// Create node
// -----------
auto* pNode = new (pmReserved) NodeType{std::forward< ParamTypes >(aParams)...};
mNodes.emplace_back(pNode);
return *pNode;
}
private:
std::size_t mMemorySize {1024};
MemoryStorage mMemory {std::make_unique< std::byte[] >(mMemorySize)};
std::byte* pmReserved {mMemory.get() + mMemorySize};
NodeStorage mNodes {};
};
In C++, we can constrain the type parameters used to specialize our templates using concepts.
If we attempt to specialize our nodes with a type that does not meet these constraints, a compilation error will occur.
For our behavior tree, we will create a concept where the typename must be a type derived from the node interface we have defined.
template < typename T >
concept BTNodeType = std::derived_from< T, CBehaviorNode >;
template < BTNodeType NodeType, typename... ParamTypes >
NodeType& CreateNode(ParamTypes&&... aParams)
{
// Error if BTNodeType is not derived from CBehaviorNode
// -----------------------------------------------------
}
Similar to decision trees, creating groups of nodes would be straightforward and clean to build in our application.
For example, we can design a sequence node that handles path following through various waypoints using the arrive steering behavior in a node format.
Tree.CreateNode< CBehaviorNodeSequence >
(
&Tree.CreateNode< CBehaviorActionArrive >( Point2D{100.0, 50.0} ),
&Tree.CreateNode< CBehaviorActionArrive >( Point2D{400.0, 50.0} ),
&Tree.CreateNode< CBehaviorActionArrive >( Point2D{400.0, 300.0} ),
&Tree.CreateNode< CBehaviorActionArrive >( Point2D{100.0, 300.0} )
);
Another example using the selector node could involve combining several sequence nodes.
One sequence node handles the path we've previously discussed, while another uses a boolean node to decide whether to move towards a position (such as a health pack or ammunition).
If the action cannot be completed (i.e., the boolean returns false), the selector node will switch to the next sequence node to start the path.
Tree.CreateNode< CBehaviorNodeSelector >
(
&Tree.CreateNode< CBehaviorNodeSequence >
(
&Tree.CreateNode< CBehaviorBooleanDecision >( true ),
&Tree.CreateNode< CBehaviorActionArrive >( Point2D{500.0, 50.0} )
),
&Tree.CreateNode< CBehaviorNodeSequence >
(
&Tree.CreateNode< CBehaviorActionArrive >( Point2D{100.0, 50.0} ),
&Tree.CreateNode< CBehaviorActionArrive >( Point2D{400.0, 50.0} ),
&Tree.CreateNode< CBehaviorActionArrive >( Point2D{400.0, 300.0} ),
&Tree.CreateNode< CBehaviorActionArrive >( Point2D{100.0, 300.0} )
)
);
 Carlos Peña
Carlos Peña